特殊相対性理論によれば、動いていると時間の進みが遅くなります。
ところが「どちらが動いているか」は、あくまで相対的なものであるために
・ＡさんからＢさんを見たときは、Ｂさんの時間が遅れ
・ＢさんからＡさんを見たときは、Ａさんの時間が遅れる
という、わけがわからないよ状態になることを前回まで書きました。

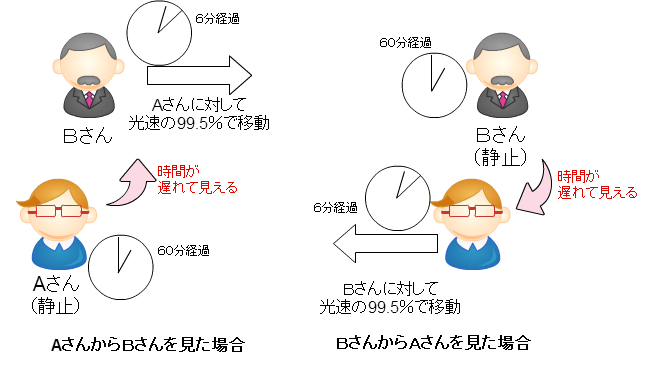
これは「双子のパラドックス」とも言われる、有名なパラドックス（矛盾）です。
なぜ「双子」と言うのかといえば、話をおもしろくするために、ＡさんとＢさんは双子という設定にするからです。
というわけで、ここでもＡさんとＢさんは双子ということにします。
どう見てもＢさんの方が歳を食っているように見えますが、人を見かけで判断してはいけません！ヒゲが生えているからです、きっと。

ここで、こんな疑問が生まれます。
「ＡさんとＢさんに、それぞれ時計を持たせて、後で比べたら、結局どちらの時計が遅れてるのだろう？？」

結論から言うと
動くスピードや方向を変えているＢさんの時計が遅れるのですが、それについて説明します。

■「比べる」には、同じ場所にいなければならない

まず「比べる」には、同じ場所にいる必要があります。

日本にいるＡさんの時計と、アメリカにいるＢさんの時計を比べようとしても、できませんね。
Ａさんがアメリカに行くか、Ｂさんに日本に来てもらう必要があります。

「電話かメールすりゃいいじゃん！」と思うかも知れませんが、電話でもメールでも、「情報」を伝えるには、その情報をもった”何か”を相手まで届ける必要があります。
手紙ならば手紙、電話やメールならば電気信号を送るわけですが、「どんな物質も光より速く動くことはできない」と相対性理論からわかっていますから、情報の伝達スピードには、光の速度という上限があるわけです。

もちろん光で伝えるのが一番速いわけですが、そうなると光速度不変の原理などから色々ややこしいことが出てくるのです。
というか、冒頭で述べた
・ＡさんからＢさんを見たときは、Ｂさんの時間が遅れ
・ＢさんからＡさんを見たときは、Ａさんの時間が遅れる
というのが、まさに光で情報をやりとりしたときに起こる現象なのです。
（このブログでは基本的に式は書かないので、数式で知りたい人は本などお読みください）

そのため、ＡさんとＢさんの時計を比べたければ、２人が同じ場所にいる必要があります。
（時計だけ同じ場所にあれば、いいんじゃない？と、ツッコむ人もあるかもですが、本質的に同じだということは書く必要ないですよね？？）

あるいは時空を超えたテレパシーとかをＡさんとＢさんがお互い使えればいいのですが、今回はＡさんもＢさんも、ふつーの一般人ということで、カンベンしてください。

■「比べる」には、加速・減速が必要

まず、ＡさんとＢさんが同じ場所で時計をあわせてから、Ｂさんが出発するとしましょう。
ここでＢさんは、実は改造人間で、奥歯のスイッチを噛むことで、光速の99.5％まで加速できることにします。
それならテレパシーくらい使えそうですが、あくまで一般人です。Ｂさんの動きを見てみると

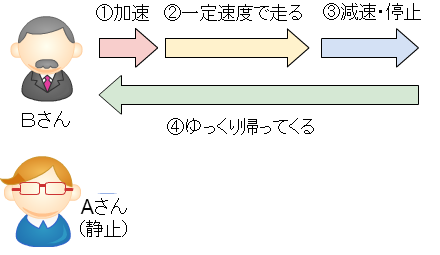
１．Ｂさんは、どんどん加速していきます。
２．光速の99.5％まで加速したら、そのまましばらく走ります。
３．このままだとＢさんは宇宙の彼方までいって帰ってきませんので、適当なところで減速します。
４．そのあとは（相対性理論の効果が無視できるくらい）ゆっくり帰ってくるとしましょう。

※よくある設定では、４でゆっくり帰ってくるのではなく、Ａさんの方に向かって加速→等速直線運動→減速をするのですが、時間の遅れが２倍になるだけなので、ここでは、ゆっくり帰ってくることにします。

実はこのとき、特殊相対性理論をそのまま適用できるのは「２」のときだけです。（もちろん４もだけど無視）

というのも、特殊相対性理論の原理（前提）を思い出すと
・光の速度は常に変わらない（光速度不変の原理）
・電気と磁気の法則は、止まっている物体でも等速直線運動をしている物体でも同じ（特殊相対性原理）
というものでした。

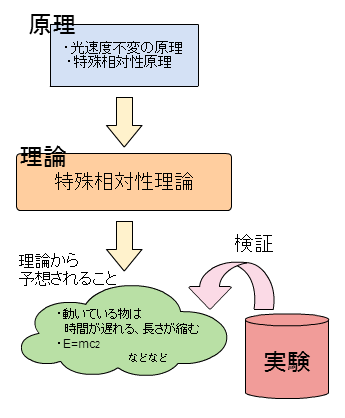
この「特殊相対性原理」をよく見ると、”等速直線運動”と書いてあります。
ということは、スピードが変わったり（等速じゃない）、動く方向が変わったりする（直線じゃない）場合には、特殊相対性理論は使えないのです！
こうした場合は、一般相対性理論を使わねばなりません。

なので実は「時計を比べる」ときには、一般相対性理論の効果も入れねばならなくなってくるのです。

※ただし、一般相対性理論を認めてしまえば、加速・減速中の時間の遅れも、特殊相対性理論の場合と同じ式が使えるので、Wikipediaの説明では特殊相対性理論の式が使われています。

で、それも踏まえて考えると、結局、時間が遅れるのはＢさんの方になります。

■慣性力（かんせいりょく）がカギ！

Ｂさんの方の時間が遅れる理由を「一般相対性理論の効果だ！」とボカして書きましたので、これについてもうちょっと説明を加えます。

１～３のステップを、Ａさんの視点から見ると、Ｂさんは
１．加速
２．等速直線運動
３．減速
と動いているように見えるはずです。

対して、Ｂさんから、Ａさんを見たときにも
１．加速
２．等速直線運動
３．減速
と見えるはずです。

これだけ見ると、まったく同じで対称的なのに、どうしてＢさんの方の時間が遅れることになるのか。

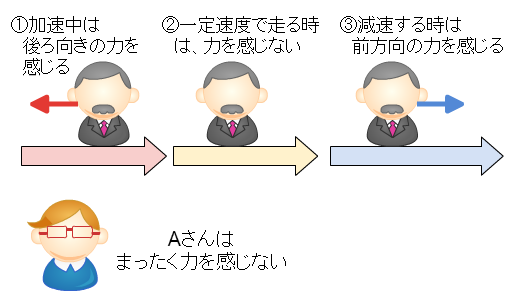
その秘密は、Ｂさんが加速（１）や減速（３）をしているとき、本当は動きが対称じゃないからです。
なぜなら、このとき、Ｂさんは力を感じているはずだからです。

車や電車に乗っていると、加速するときには後ろに引っ張られる力、減速するときには前につんのめりそうになる力を感じると思います。
満員電車で目の前にきれいなお姉さんが乗っているときに急ブレーキがかかると、ついお姉さんの方につんのめってしまって美味しい思いができるといいなー、と思いつつ
現実には目の前にいるのはオッさんで、オッさんのハゲ頭にぶつかってしまうというあの力です。
この力は　【慣性力（かんせいりょく）】　と呼ばれるもので、加速したり、減速したり、あるいは動く向きが変わったとき（これらをまとめて「加速度が０でないとき」と言います）に感じる力です。

Ｂさんが加速（１）や減速（３）をしているとき、Ｂさんはこの慣性力を感じます。
一方、Ａさんが慣性力を感じることはありません。だって加速したり、減速したりしているのはＢさんですから。隣の人が走り出したからといって、自分が急に後ろに引っ張られることはないのと同じです。
つまり、ここで、ＡさんとＢさんの動きは対称ではないことが分かります。

これがＢさんの方の時間が遅れる理由です。

これを一般相対性理論から説明すると、加速・減速・運動の方向が変わるとき（加速度が０でないとき）には、時間が遅れるので、結局、時間が遅れるのはＢさんの方になります。

■今日のまとめ

・あとから時計を比べる場合、加速・減速・運動の方向が変わる側（加速度が０でない側）の時間が遅れる！

※細かい計算が気になる方は、Wikipediaか物理の本をお読みください。