前回(相対性理論について普通の人の3倍詳しくなる話)までで
【特殊相対性理論】とは
1.「光速度不変の原理」光の速さは常に変わらない
2.「特殊相対性原理」電磁気の法則は、止まっている物体でも、等速直線運動している物体でも変わらない
の2つの原理を元に導かれる理論だというお話をしました。
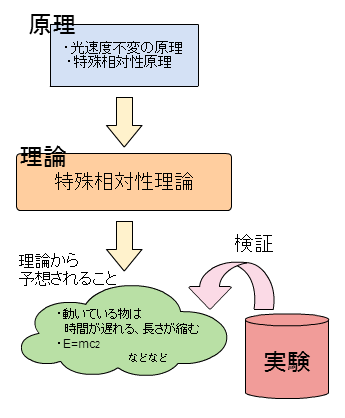
物理の教科書ならば、ここで方程式を書いたりするわけですが、
おそらくこれを読んでいる方の99%は、方程式に興味などないと思いますので、相対論が示すこの世界の予想について見ていきましょう。
※式の導出までやりたい人は、そういう教科書などを読んでみてください。
理系学生なら、大学2,3年で学ぶ内容なので、そこまで難しくはないです。
まず最初は、物理学でもっとも有名な式といわれる
E=mc2
について、その意味を考えていきます。
相対性理論から導かれるこの式は、シンプルながら奥深い意味を持ちます。
■エネルギーと質量はお互いに変わる
E=mc2
シンプルでありながら、深い意味をもつこの式は多くの人々を魅了してきました。
座右の銘にしたり、名刺に書いたり、芸名にしたりなど、多くの使い道のあるこの式は
今日、子供でも知っており、小学校ではE=mc2ごっこも大人気です。(ウソです)
左辺のEとは、エネルギー(Energy)のこと。
右辺のmは、質量(Mass)であり
cは光の速さ(=約30万km)をあらわします。
なぜ、光の速さをcであらわすのか?というと、歴史的な経緯があります。
最初に、電磁気学の発展に貢献したヴィルヘルム・ヴェーバーという人が、ヴェーバー定数cというものを定義しました。
このcが、実は後に光速と等しいことが分かりまして、今日、ヴェーバーの使ったcという記号が光速を表す記号になっています。
ついで、に後付け感がありますが、ラテン語で「速さ」をあらわす celeritas という言葉のcという意味もあるそうです。
つまり、この式は、
エネルギー = 質量
ということを表しています。
右辺のc2cは、単位をあわせているだけなので、あまり気にする必要はありません。
エネルギーの単位は、(質量)×(長さ)2÷(時間)2なので、c2をかけることで両辺の単位が一致するのです。
なので、この式は
エネルギーと質量はお互い移り変わる
ということを意味します。
質量がエネルギーに変わる(右辺→左辺)例としては
原子爆弾や水素爆弾、原子力発電などがあります。
c2という非常に大きな数が右辺にあることから分かるように、ほんのちょっとの質量が莫大なエネルギーに変わります。
エネルギーが質量に変わる(左辺→右辺)という例としては
粒子のスピードをどんどん上げていく(運動エネルギーを増やしていく)と、その粒子から別の粒子が飛び出すことが知られています。
少し前にニュースになった「ヒッグス粒子の発見」では、二つの水素原子のスピードを上げて(運動エネルギーを与えて)ぶつけることにより、そのエネルギーからヒッグス粒子が作られる現象をたしかめる実験が行われました。
つまり僕らが通常「モノ」と思っているものも、実はエネルギーの塊であるという見方ができます。
いや、何より僕らの体や脳だって、エネルギーの塊と見ることができるわけです。
バカ殿も、天使すぎるアイドルも、松岡修造もみなエネルギーの塊です。
どうりで暑苦しいわけだ。
■動いているときは、E=mc2じゃない!?
実は、E=mc2が成り立つのは、その物体が止まっているときだけです。
動いているときには
E2 = m2c4 + p2c2
という式が成り立ちます。
ここでpとは、その物体の運動量(≒質量×速さ)のことです。
物体が止まっているときには、p=0なので、E2=m2c4となり、E=mc2となるわけです。
知ったかぶりしたいときに使える知識ですね!
E2c = m2c4 + p2c2
という式から分かるのは、物体のスピードが上がる(pが大きくなる)ほど、エネルギーEも大きくならねばならない、ということです。
つまり、物体のスピードを上げる(運動量pを大きくする)ほど、
それに見合うだけのエネルギーを物体に与えねばならないことを意味しています。
※理系学生向けに
普通の式ならば、E2c = m2c4 + p2c2とは、pが与えられたときにEを計算する式であり、
pが大きくなればEも”自動的に”大きくなることを意味する。
しかし相対性理論でのこの式は、Eとpが満たすべき関係式であり、
pを大きくするにはEも大きくせねばならないことを意味する。
特に、物体のスピードが、光速に近づくほど、運動量pは無限に大きくなることが、カンタンな計算で示せます。
とういことは、物体のスピードを光速に近づけようとするほど、より大きなエネルギーが必要となるため、物体のスピードは光速より常に遅くなることが分かります。
ただし、これは質量のある粒子の場合の話。
質量0の場合は、運動量の計算が違ってきます。
その計算をすると、質量0の粒子の速度は常に光速であるということが導かれます。
ということは、
この宇宙において、光速よりも早く動く物質は存在しない
というわけです。
■今日のまとめ
E=mc2(本当はE2=m2c4+p2c2)から分かることとして
・エネルギーと物質は相互に移り変わる
・質量0の粒子は、常に光速であり
質量がある粒子の速度は、常に光速より遅い